Example: How to Solve an Initial Value Problem (Exponential Growth)
- Find the solution of the differential equation dy/dt=2y that satisfies y(0)=1.
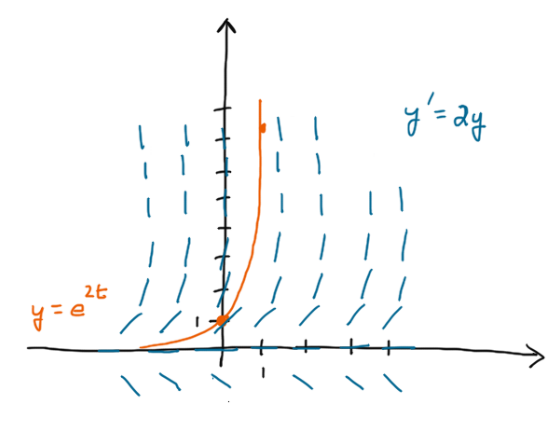
- Sketch the graph of the solution along with the slope field for dy/dt=2y.
- Terminology:
- What do we call a problem such as dy/dt=2y, y(0)=3?
- What do we call the equation y(0)=3?
- Solve dy/dt=(1/3)y, y(0)=2 (Use a formula to find the solution quickly.)
Answer:
The solution is y=e^(2t). In the video, a full explanation is given for how this solution is derived. Near the end of the video, you'll learn a formula based on this derivation that will enable you to quickly solve the important differential equation dy/dt=ry for any constant r.
The graph of the solution, along with the slope field.
- Terminology:
- We call this an initial value problem.
- We call this the initial condition.
- The solution is y=2e^((1/3)t).